自動車整備士.com
複数条件の場合はキーワードの間にスペースを入れてください。Advertisement
時定数(ときていすう・じていすう)
定常状態の63%に要する時間を時定数と理解しておけばokです。
下手に認定教科書に書かれたものですから、説明しなければならない羽目になったようなものです。
以下、適当に読み流してください。(たまにはちょっとカッコつけて書きました。![]() )
)
二級ガソリンのテキスト(日本自動車整備振興会連合会)における電子制御装置の説明の中で、「時定数」という用語が使われている。
「じていすう」と呼ばれているが、定義上は「ときていすう」であり、その単位は「秒」である。
自動車整備士試験に「ときていすう」の問題が出題されることはないと思われるが、装置を理解する上で必要な知識であるから、これらについて考えてみる。
下の表は、インジェクタのスペックの一部である。
| 項 目 | 標準 |  |
|
| (1) | コイル抵抗 | 13.5Ω(500T) | |
| (2) | インダクタンス | 17.7mH | |
| (3) | 開弁応答性 | 1.26ms | |
| (4) | 閉弁応答性 | 0.646ms |

◆インジェクタの時定数の例
上記スペックのコイルの抵抗は 13.5Ω、自己インダクタンスは17.7mHとなっている。
インジェクタは電気回路としては、抵抗とコイルが直列接続されたR-L回路として扱うことができる。
この回路の時定数τ(タウ)は、次式となる。
| τ = | L
R |
[秒] |
この式の意味は、時定数は電流の立ち上がりの程度を表しており、時定数を小さくするには、コイルの自己インダクタンスを小さくすればよいことになる。
また、インジェクタのソレノイド・コイルに導線抵抗Rが大きいものを使用しているものは、高抵抗型インジェクタと呼ばれており、電流を小さくし発熱防止というメリットがあるが、時定数を考慮したうえでのものである。
さて、計算してみる。
| τ = | 17.7×10-3
13.5 |
=1.31×10-3 | =1.31[ミリ秒] |
上のサンプルでは、開弁応答性 1.26msとなっていますが、開弁応答性の定義が分かりませんが、計算した結果と近い値になっています。
開弁応答時間については、プランジャの作動応答の問題を含むので解析が厄介になるため、ここでは電気的な応答だけを問題にする。
◆R-L回路
数式はすこし難しいが、R-L回路の特徴についてまとめてみる。
コイルは、電流が一定であると、抵抗は0と同じであるが、下記回路のS1をONにすると、バッテリ電圧εが印加されが、コイルに生じる逆起電力のため始めは電流が流れない。
時間が経つにつれて電流は大きくなる。
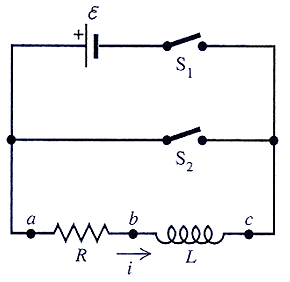
この時の電流は、
| L・ | di(t)
dt |
+ | R・i(t) | = | ε(t) | (1) |
の微分方程式の解より、
S1をONにしてt秒後の電流iは、
| ε | -(R・t/L) | |||
| i(t)= |
|
(1-e ) (2) | ||
| R | ||||
となる。
S1をONにした直後は、コイルに流れる電流iは0になり、電流が増加し最終的には電流はε/Rまで増加する。
この関係をグラフに表すと下図のようになる。
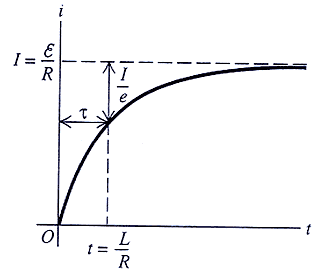
式(2)において、t=τを代入すると、
| ε | -1 | |||
| i(τ) | = |
|
(1-e )≒ 0.632・I [A] | |
| R | ||||
となる。
すなわち、時定数τとは、定常電流I[A]=ε/Rの63.2%に達するまでの時間を意味する。
実用的には、自己インダクタンスとコイル抵抗が分かれば、回路の大雑把な応答時間が分かるというものである。
電流がI0の時、回路においてS1を開き、S2を閉じたときの電流は次のようになる。
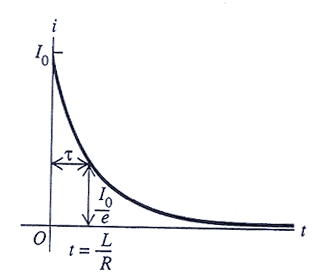
| ε | -(R・t/L) | ||
| i(t)= |
|
e | |
| R | |||
| τ= | L
R |
の単位はなぜ [秒] なのか |
”時定数”とは、なかなか洒落た用語ではないか。
時をつかさどる神秘的なニュアンスを感じないわけでもないが、さて、コイルと抵抗の割り算がなぜ「秒」になるのであろうか。
SI は、四つの基本量としての MKSA単位--長さ:メートル(m)、質量:キログラム(kg)、時間:秒(s)、電流:アンペア(A)--を基本として、これに温度の単位としてケルビン(K)、物質料:モル(mol)、光度:カンデラ(cd)を基本単位とする。
また、補助単位としては平面角:ラジアン(rad)、立体角:ステララジアン(sr)を認めている。
他は全て組立単位である。
例えば力の単位はニュートン(N)で、上の基本単位で組み立てられる。
「力」は加速度と質量の積で F=m・g だから、kg・m/s2 で組み立てられる。
まず、コイルの自己インダクタンスをMKSAで表現してみよう。単位はヘンリHである。
| H= | Wb
A |
、 | Wb=V・s | |
Wb;ウェーバー(Weber)
抵抗R[Ω]をMKSAで表すためには、R=V/Aであるから、問題となるのはVをいかに表すかである。
| V= | J
C |
、 C=A・s、 J= | m2・kg
s2 |
||||
C;クーロン(Coulomb)
結局、次のように、時定数の単位は秒になる。
| H | = | m2・kg
s2・A2 |
、 | Ω | = | m2・kg
s3・A2 |
| H | s2・ |
s3 | |||||
| τ= |
|
= |
|
= |
|
=s[秒] | |
| Ω | s3・ |
s2 | |||||
電気の分野ではここで述べたR-L回路とR-C回路のみに”時定数”は用いられる。
モータ制御の分野では”機械的時定数”という用語が用いられ、
その定義は「無負荷状態で電圧を印加して、無負荷回転数の63%までに加速するのに要する時間をいう。」が一般的であり、ここでも63%がひとつのめやすになっている。
◆まとめ
すこし、難しくなったついでにまとめると、次のようになる。
電気や自動車、流体系すべての分野において、入力と出力の関係が式(1)の一階線形微分方程式で表される要素すべてを制御の分野では、”一次遅れ要素”と呼んでいる。
その挙動は、すべて同様な振る舞いをする。
この一次遅れ要素において、定常状態の63%に要する時間を時定数と呼んでいるのである。
インジェクタも瞬間的な挙動を解析する過渡現象的には一次遅れ要素であるが、スイッチの”オン”、”オフ”として用いる場合には、単なるバルブであり、難しいことは考えなくてよい。
ただ、コイルの逆起電力や電流の立ち上がりを考察する場合には、時定数という概念は具体的な時間を知り得るという意味で極めて重要なものである。
Today Yesterday
Total