自動車整備士.com
複数条件の場合はキーワードの間にスペースを入れてください。Advertisement
パワー・シリンダの圧力
図のパワー・シリンダに500 kPa の圧力をかけたとき,ハイドロリック・ピストンを押す力として, 適切なものは次のうちどれか。なお,円周率は3.14 とする。

解説
選択肢(3)が適切です。
おなじみのパスカルの原理です。
密封した液体の一部に圧力を加えると他の全ての箇所において同じ圧力が生じる。
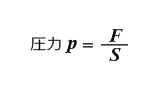
どこでも圧力がいっしょですから、 ピストンの面積を変えれば力を変えらるということになります。
しかし、この問題は、力を倍増する問題ではありません。
内径のデータが二つありますので、うっかり引っかかってしまいそうですね。
この問題はパワーシリンダの圧力が与えれていますので、パワー・シリンダの力Fを求めます。
すなわち、この力がハイドロリック・ピストンを押す力になります。
工学系の距離の単位はメートルです。
ミリメートルとメートルの変換がひっかけともいえます。
面積計算は、
半径[m]×半径[m]×3.14
ですが、直径が200mmですから、
半径が100mm、すなわり0.1mになります。
F =p×S[m2]
=500kPa×3.14×(0.1×0.1)
=15700N
となります。
Advertisement
Today Yesterday
Total