整備士ドットコム
Jidoshaseibishi.com
複数条件の場合はキーワードの間にスペースを入れてください。2級自動車整備士・試験問題
パスカルの原理
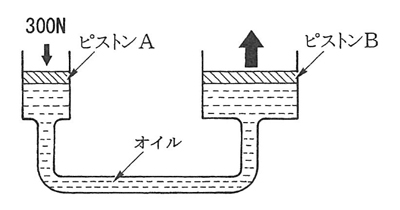
図に示す油圧装置でピストンAの直径が25mm、ピストンBの直径が75mmの場合、ピストンAを300Nの力で押したとき、ピストンBにかかる力として、適切なものは次のうちどれか。
解説
選択肢(3)が適切です。
おなじみのパスカルの原理です。
密封した液体の一部に圧力を加えると
他の全ての箇所において同じ圧力が生じる。
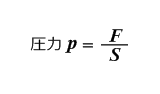
どこでも圧力がいっしょですから、ピストンの面積を変えれば力を変えらるということになります。
\[ \begin{align*} \frac{F_1}{S_1}=\frac{F_2}{S_2}= p \hspace{10pt} 一定 \end{align*} \]
の関係から、
\[ \begin{align*} F_2 = \frac{S_1}{S_2} F_1 \end{align*} \]
となります。
ここでポイントは題意は、ピストン直径が与えられていますから、面積計算を間違わないようにしなければなりません。
上の式のように面積比ですから、半径掛ける半径掛ける3.14は、分母分子でキャンセルされ、結局、直径比の二乗になることに注目します。
比というのは、単位がミリでもセンチでもさらには半径でも直径でも上下同じにしておけばなんでもいいので、便利といえば便利です。
ただし、二乗することを決して忘れないでください。
それがこの問題のヒッカケと言えばヒッカケです。
要注意です。
だから選択肢(1)に単純に3倍(75/25)した
900=0.9kN
を手ぐすね引いてヒッカケようとして待ち構えています。
用心、用心。
\[ \begin{align*} F_2 &= \left( \frac{75}{25} \right)^2 \times 300 \\ \\ &=\left( \frac{3}{1} \right)^2 \times 300 \\ \\ &=9\times 300 \\ \\ &=2700 \\ \\ &=2.7kN \end{align*} \]
となります。
2G 登録試験 2012年10月 問題34 油圧式ブレーキの油圧回路