整備士ドットコム
Jidoshaseibishi.com
複数条件の場合はキーワードの間にスペースを入れてください。2級自動車整備士・試験問題
電気回路計算問題(接触抵抗)
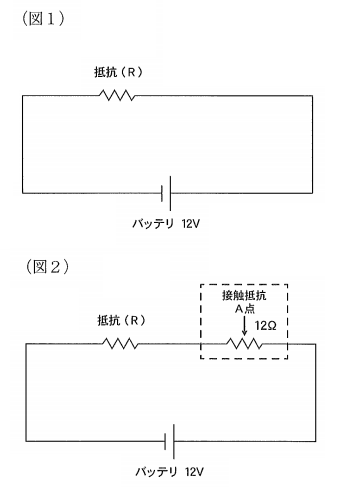
図1に示す回路において、抵抗(R)の電力は12Wである。いま、図2に示すように、A点に12Ωの接触抵抗が発生したときの抵抗(R)の電力として、適切なものは次のうちどれか。ただし、バッテリ及び配線の抵抗はないものとする。
解説
電気回路的には、接触抵抗を一つの抵抗器とみなしますから、二つの抵抗が直列接続されたものとして取り扱います。
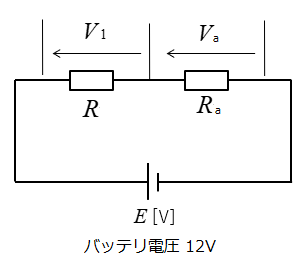
接触抵抗:Ra
元の抵抗:R
Rの両端電圧(分担電圧):V1
Raの両端電圧(分担電圧):Va
Rの電力:P1
Raの電力:Pa
図1のRの値を求めておきます。
$$ P_1 = \frac{V_1^2}{R} \tag{1} \\ $$より、
\[ \begin{align*} R = & \frac{V_1^2}{P_1} \\ \\ = & \frac{12 \times \cancel{12}}{\cancel{12}} \\ \\ = & 12 \Omega \\ \end{align*} \]
図2におけるRの両端電圧(分担電圧)V1は、同じ12Ωの抵抗が直列接続されていますので、6Vになることは容易にわかります。
とりあえず、計算式も示しておきましょう。
\[ \begin{align*} V_1 = & \frac{R}{R + R_a} \times E \\ \\ = & \frac{12}{12+ 12} \times 12 \\ \\ = & \frac{ \cancel{12}}{ \cancel{24}} \times 12 \\ \\ = & 6 V \\ \end{align*} \]
式(1)より、Vの電力P1を求めます。
\[ \begin{align*} P_1 = & \frac{V_1^2}{R} \\ \\ = & \frac{6 \times 6}{12} \\ \\ = & \frac{36}{12} \\ \\ = & 3 W \\ \end{align*} \]
選択肢(2)が適切ということになります。
同じ12Ωの抵抗が接続されているから、もとの電力が12Wだから半分ずつで6Wであると判断しないでください。
電力とは、電圧のエネルギと電流のエネルギを掛け合わしたものです。
抵抗が12Ωから24Ωに増加した分、電流が減少し、さらにかかるべき電圧も半減したために12Wから3Wにまでに、すなわち、1/4にまで抵抗での消費電力は減少しました。
この問題は、接触抵抗があると、受けるべき電力が半減、それ以上に減少することを述べています。