整備士ドットコム
Jidoshaseibishi.com
複数条件の場合はキーワードの間にスペースを入れてください。2級ガソリン・ジーゼル自動車整備士・試験問題
電気計算(Open closed 問題)
図に示す電気回路と各抵抗値において、次の文章の( )に当てはまるものとして、適切なものは次のうちどれか。ただし、バッテリ、スイッチ及び配線の抵抗はないものとし、電圧計Vの内部抵抗は20kΩとする。
スイッチの接点が開いているとき、電圧計Vが6Vを示している。次に、スイッチの接点が閉じたとき、電圧計Vが示す値は( )である。
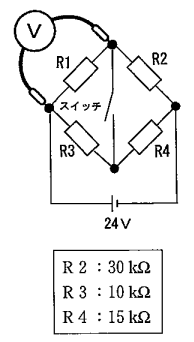
解説
選択肢(2)が適切です。
主に分圧の法則を用いながら解いてみましょう。
内部抵抗20kΩの電圧計と抵抗R1の並列接続部分は、これをRと置いておきましょう。
R1を求める必要はありませんので、20kΩはダミーのデータです。
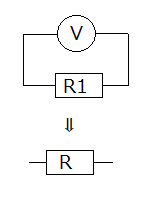
スイッチoff の状態ですから回路は次のようになります。

並列接続ですから、回路の半分で電圧分配(分圧の法則)を考えます。
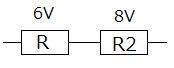
あるいは。
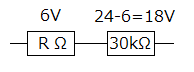
オームの法則 $ V=R \times I $は、電圧と抵抗は比例関係にありますので、直列接続の電圧と抵抗との比で$R$を求めてみます。
\[ \begin{align*} R : 30k = & 6 : 18 \\ \\ 18 \times R = & 30k \times 6 \\ \\ R = & \frac{ 30k \times \cancel{ 6}} { \cancel{18}} \\ \\ = & \frac{ 30k} {3} \\ \\ = & 10k \Omega \\ \end{align*} \]
スイッチonの状態での回路図を書き直すと次のようなります。
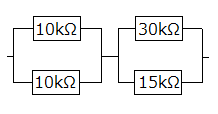
回路左側の計算です。
\[ \begin{align*} \frac{1}{10k} + \frac{1}{10k} & = \frac{1 + 1}{10k} \notag \\ \\ & = \frac{2}{10k} \notag \\ \\ \text{ゆえに } & 5k \Omega \\ \end{align*} \]
回路右側の計算です。
\[ \begin{align*} \frac{1}{30k} + \frac{1}{15k} = & \frac{1}{30k} + \frac{2}{30k} \notag \\ \\ = & \frac{1 + 2}{30k} \notag \\ \\ = & \frac{3}{30k} \notag \\ \\ = & \frac{1}{10k} \notag \\ \\ ゆえに & 10k \Omega \\ \end{align*} \]
ここまでを整理し、回路を書き直します。
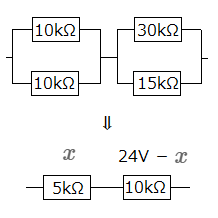
またもやオームの法則 $ V=R \times I $は、電圧と抵抗は比例関係にありますので、比で$5k\Omega$の両端電圧$x$を求めてみます。
\[ \begin{align*} 5k : 10k = & x : 24-x \\ \\ 10k \times x = & 5k \times(24-x) \\ \\ 10k \times x = & 5k \times 24 - 5k \times x \\ \\ 10k \times x + 5k \times x = & 5k \times 24 \\ \\ 10 \cancel{k} \times x + 5 \cancel{k} \times x = & 5\cancel{k} \times 24 \\ \\ (10+5) x = & 5 \times 24 \\ \\ 15 x = & 5 \times 24 \\ \\ x = & \frac{ \cancel{5} \times24 } { \cancel{15} } \\ \\ = & \frac{24}{3} \\ \\ = & 8V \\ \end{align*} \]
この作戦は、部分的な並列接続部をまとめれば、回路全体として結果的に直列接続の形をとっていると分圧の法則を適用し電流計算(分流の法則)を避けられるという特徴があります。
別法 電流を用いる方法
戦略としては、抵抗一つひとつに部分的にオームの法則、分流の法則、分圧の法則を駆使し計算を展開する手法です。
スイッチoff の状態ですから回路は次のようになります。

並列接続ですから、回路の半分で電圧分配を考えます。

あるいは。

ここから$R$を流れる電流$I$を求めます。
\[ \begin{align*} I = & \frac{24}{R + 30k} \\ \end{align*} \]
$6V$がかかっている$R$をオームの法則により求めます。
\[ \begin{align*} R = & \frac{V}{I} \\ \\ = & \color{blue} {\frac{ \overbrace{R+30k}^{ \color{red}{\boldsymbol{電流Iの逆数}} }} {24} } \times 6 \\ \\ 24 \times R = & 6 \times R + 30k \times 6 \\ \\ 24 \times R - 6 \times R = & 30k \times 6 \\ \\ (24-6)R = & 30k \times 6\\ \\ 18 \times R= & 30k \times 6 \\ \\ R = & \frac{30k \times \cancel{6}}{\cancel{18}} \\ \\ = & 10k \Omega \end{align*} \]
細かく計算して確認してみましょう。
まさに回路を部分的にオームの法則、分流の関係、分圧の法則を織り交ぜながら緻密に求め上げて行きます。
電圧計の値が$6V$ですから、$R$2には$24-6=18V$の電圧がかかっています(分圧の法則)。
であれば、$R2$に流れる電流は$18V/30kΩ=0.6mA$となります(オームの法則)。
電流計には$6V/20kΩ=0.3mA$の電流が流れることになりますので、$R1$は$0.6mA-0.3mA=0.3mA$の電流が流れます(分流の法則)。
したがって、$R1$は$6V/0.3mA=20kΩ$となり、電圧計の内部抵抗値と同じということがわかります。
結果的に$R1$と電圧計の内部抵抗による並列接続部の合成抵抗は、$10kΩ$です。
ちなみにこの問題では、$R3$も$10k\Omega$としてあり、計算しやすくしてくれています。
ここまでを整理し、回路を書き直します。

回路電流$I$は、$I=24V/(5kΩ+10kΩ)$から、$24V/15kΩ$となります。
$5k\Omega$の電圧$V_1$を求めるには、電圧を抵抗で割ってあげればいいわけです。
\[ \begin{align*} V_1 = & 5k \times I \\ \\ = & 5k \times \frac{24}{5k + 10k} \\ \\ = & \cancel{5k} \times \frac{24}{\cancel{15k}} \\ \\ = & \frac{24}{3} \\ \\ = & 8V \end{align*} \]
最近の出題傾向としては、簡単な電気回路計算では飽き足らず、少しずつ手間がかかる問題になりつつあります。
工学分野の責任点がありますので、落とすことなく確実に点数をゲットしてください。