整備士ドットコム
Jidoshaseibishi.com
複数条件の場合はキーワードの間にスペースを入れてください。2級ガソリン自動車整備士・試験問題
2G 登録試験 2024年10月 問題17
トルク・コンバータに関する記述として、適切なものは次のうちどれか。
解説
(1)コンバータ・レンジでは、全ての範囲において速度比に比例して伝達効率が上昇する。
選択肢(1)は不適切です。
正しくは、以下の通りです。
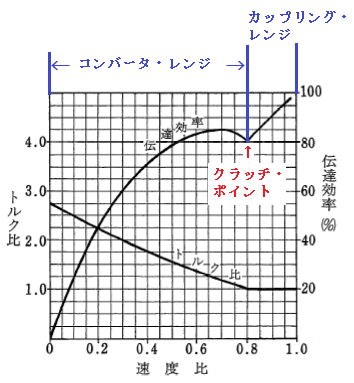
カップリング・レンジでは、速度比に比例して伝達効率が上昇する。
出力は、トルクと回転速度に比例するため、コンバータ・レンジで伝達効率は急上昇するが、タービン・ランナからのATFがステータの羽根の裏側に当たるようになると、伝達効率は落ち始める。しかし、その後カップリング・レンジでは、速度比に比例して伝達効率が上昇する。
(2)速度比がゼロのときの伝達効率は100%である。
選択肢(2)も不適切です。
正しくは、以下の通りです。
速度比がゼロのときの伝達効率は0%である。
(3)カップリング・レンジにおけるトルク比は、2.0~2.5である。
選択肢(3)も不適切です。
正しくは、以下の通りです。
カップリング・レンジでのトルク比は1である。
(4)速度比は、タービン軸の回転速度をポンプ軸の回転速度で除して求める。
選択肢(4)が適切です。
\[ e\rm{:}速度比 = \frac{タービン軸回転速度(出力) }{ポンプ軸回転速度(入力)} \\ \]
【参考】
トルク・コンバータの出力トルクの計算には、複雑な要素が関係しています。
代表的な式として、以下のような計算式が使用されます:
\[ T_o = N_p ^{²} · p(e) · t(e) · r(G_p) · g_f \]
ここで、
- $T_o$: 出力軸トルク
- $N_p$: エンジン回転数(ポンプ・インペラの回転数)
- $p(e)$: トルク・コンバータのポンプ容量係数
- $t(e)$: トルク・コンバータのトルク比
- $r(G_p)$: ギア・ポジション毎のギア比
- $g_f$: ファイナル・ギア比
- $e$: トルク・コンバータの速度比($e = N_t / N_p、N_t$はタービン・ランナ回転数)
この式は以下の要素を考慮しています:
- エンジン回転数の2乗($N_p ^2$): エンジンの回転エネルギを表します。
- ポンプ容量係数 $p(e)$: トルク・コンバータの設計特性を反映します。
- トルク比 $t(e)$: 入力トルクに対する出力トルクの比率を表します。
- ギア比 $r(G_p)$: 現在のギア・ポジションでの減速比を考慮します。
- ファイナル・ギア比 $g_f$: 最終的な減速比を表します。
この式は、トルク・コンバータの特性曲線、ギアボックスの影響、そしてエンジンの出力特性を総合的に考慮しています。
実際の計算では、これらのパラメータの多くは、速度比eの関数として表されるルックアップテーブル(英: Lookup table)や特性曲線から得られます。また、エンジン・トルクやスロットル開度などの追加のパラメータも考慮される場合があります。
この計算式は、自動車の動力伝達系統の複雑さを反映しており、トルク・コンバータを通じてエンジンの出力が車輪に伝達される過程を数学的にモデル化しています。
トルク出力の式の両辺に角速度ωを掛けると、動力(パワー)の式が得られます。これは機械工学の基本的な原理の一つです。
単位は、$T_o · ω$ の単位は $[N·m·rad/s] =P_t [W]$(ワット、パワーの単位)となります。
この式は、エネルギ保存の法則を反映しています。入力パワー(エンジンからの)が、トルク・コンバータとギア・トレインを通じて変換され、最終的な出力パワーになることを示しています。
実際のシステムでは、摩擦や熱損失などによりエネルギの一部が失われます。そのため、完全な等式ではなく、効率項を含める必要があります。
したがって、トルク出力の式の両辺に角速度ωを掛けることで、動力(パワー)の式が得られます。これは、トルクと回転速度の関係が、機械的なパワーにどのように変換されるかを示す重要な概念です。
参考に長ったらしい書き方になりましたが、その理由は教科書に”出力は、トルクと回転速度に比例する”とサラリと書いてありますが、かなり重い言葉です。
すなわち、トルコンの動力$P_t$[$W$]は、トルコンの出力トルク[$N・m$]と回転数$ω$[$rad/s$]に比例するということを指します。
教科書は、トルコンの出力$P_t$[$W$]をさらっと流す達人なのです。
こんなことで妙に突っ込まれも厄介なことになりますから、ましてや二級とは関係なくなりますので、教科書も二級を勉強する人も軽くスルーするのが賢明な対応でよろしいと思います。
で、ちょっと深堀したという、落ちでございます。